Table of Contents
- Kebijakan Berbasis Data: Analisis Dan Prediksi Penyebaran Covid
- Create Nonseasonal Arima Model Template
- Methods For Time Series Analysis
- S15 Table Confusion Matrix For Predicted Weekly Positive Submissions.
In this work we introduce the class of beta autoregressive fractionally integrated moving average models for continuous random variables taking values in the continuous unit interval $$. The proposed model accommodates a set of regressors and a long-range dependent time series structure. We derive the partial likelihood estimator for the parameters of the proposed model, obtain the associated score vector and Fisher information matrix. We also prove the consistency and asymptotic normality of the estimator under mild conditions. Hypotheses testing, diagnostic tools and forecasting are also proposed.
Both demographic and aggregate COVID-19 data in the DKI Jakarta Province are processed and analyzed to provide information about the current situation and conditions related to the COVID-19 pandemic in the DKI Jakarta Province. The COVID-19 data also functions to perform predictive analysis in determining estimated number of COVID-19 cases in the future. The predictive analysis used in this article is the Autoregressive Integrated Moving Average method.
An additional, alternative approach for modeling count data is to use random forest models as developed by Breiman . RF models offer a rule-based methodological approach that recursively partition data, creating regression trees. RF models have been successfully applied in many fields, including public health studies.
Kebijakan Berbasis Data: Analisis Dan Prediksi Penyebaran Covid
where ΘP, θp, ΦQ and ϕq are polynomials of order P, order p, order Q and order q, respectively. D and d represent the order of trend differencing and seasonal differencing, which are determined when the original time series is stable. In this study, the monthly incidence of human brucellosis from January 2007 to December 2016 was used to build the ARIMA model, and the process included the following steps.
The predictive accuracy of each modeling approach was evaluated via the root mean square error and the normalized root mean square error . We also assessed the models’ ability to anticipate increases and decreases in the number of diagnostic submissions and positive virological submissions at weekly and monthly intervals. Another approach developed by Davis et al. uses generalized linear autoregressive moving average models. These models accommodate time series of counts that are assumed to follow a Poisson distribution. This is the overall process by which we can analyze time series data and forecast values from existing series using ARIMA.
The MLE was used to estimate the parameters of the candidate model. According to the results of the parameter estimates and fitting index, we found that the parameters of the ARIMA 12 model were statistically significant and that the residual sequence of the model was a random sequence. In addition, the AIC and the SBC of this model were the smallest, and the R2 was the largest .
Create Nonseasonal Arima Model Template
ARCH models are commonly employed in modeling financial time series that exhibit time-varying volatility and volatility clustering, i.e. periods of swings interspersed with periods of relative calm. ARCH-type models are sometimes considered to be in the family of stochastic volatility models, although this is strictly incorrect since at time t the volatility is completely pre-determined given previous values. Autoregressive – the autoregressive value of a given time series data in their own lag, which is represented by the “P” value in the model. To the best of our knowledge, this is the only study to explore a combined model of ARIMA and ERNN for predicting the incidence of human brucellosis. Second, based on the structure of the BPNN, the ERNN adds a corresponding receiving layer in the hidden layer to provide its dynamic memory and strong sensitivity to time series, which are more suitable for analysing human brucellosis. Third, the use of the ARIMA-ERNN model contributes to rational allocation of limited public health resources and the early prevention and control of human brucellosis. From a technical standpoint, the problem with using lagged errors as predictors is that the model’s predictions are not linear functions of the coefficients, even though they are linear functions of the past data.
I get a different result with this data set using pandas.Series.autocorr over 35 lags than I do from autocorrelation_plot. Test different orders and see what works well/best for your specific dataset. Good question, I don’t have an example, but I can’t see that the ARIMA model will care about the frequency as long as it is consistent. Ideally fitting the model only when needed would be the best approach, e.g. testing when a refit is required.
This could be explained by the fact that the seasonal-naïve method ignored all predictor information. Residuals were obtained after fitting with simulated prospective autoregressive integrated moving average , generalized linear autoregressive moving average , and random forest model predicted counts at weekly and monthly intervals. The simulated prospective model results based on the LOSO cross-validation are given in S12–S15 Tables. More specifically, accuracies were 56–73%, 48–59% and 45–62% for the RF, GLARMA and ARIMA models, respectively. Additionally, the proportions of correctly identified increases found were 62–88%, 56–72% and 0–55% for the ARIMA, RF and GLARMA models, respectively. The residuals were obtained after fitting with simulated prospective autoregressive integrated moving average , generalized linear autoregressive moving average , and random forest model predicted counts at weekly and monthly intervals.
Methods For Time Series Analysis
The coefficient estimates of the retrospective ARIMA components are provided in S1 Table in the Supporting Materials. The predictive accuracy of the models is summarized in Table 1 and S2 Table.
The forecast represents the average of all such simulations at each future time. The forecast limits enclose 95% of all such simulations at each future time. Thus, an autoregressive process remembers where it was and uses this information in deciding where to go next. The most common way to estimate is through the Maximum Likelihood Estimation. It is similar to the Least Square Estimation for the regression equation, except MLE finds the coefficients of the model in such a way that it maximizes the chances of finding the actual data. Various packages that apply methodology like Box–Jenkins parameter optimization are available to find the right parameters for the ARIMA model.
- Therefore, prevention and control measures for brucellosis should consider seasonal fluctuations, and some targeted interventions should be performed at the peak of the epidemic.
- So to predict or forecast the values of certain data over a period requires specific techniques and there are many, developed over the years.
- Given count data, a Box-Cox transformation of counts using either a logarithmic or power transformation may yield approximately Gaussian-distributed data.
- To examine which p and q values will be appropriate we need to run acf() and pacf() function.
- So before prediction the current job ETA we need to predict the dependent jobs if they are not completed yet.
In this case, we are assuming the real observation is available after prediction. This is often the case, but perhaps over days, weeks, months, etc. here the steps you followed were convincing, also you have performed “inverse difference” step to scale the prediction to original scale.
Justify whether the model fulfill the stationarity and invertibility conditions. For AR model, ACF decays exponentially, and PACF is used to identify the order of AR model. If we have a significant peak at lag 1 on the PACF, then we have a first-order AR model, namely AR . If we have significant peaks of lag 1, 2 and 3 on PACF, then we have a third-order AR model, namely AR .
S15 Table Confusion Matrix For Predicted Weekly Positive Submissions.
I have the dataset at monthly level sales of product in that shop. So in this case can product Id be taken as exogenous variable in the model. I’m looking for your suggestions on TS analysis and forecasting of daily data and I use SARIMAX to fit this data. Could you please share some basic iead on this as most of the ref materials are done with monthly data and could not offer much knowledge about it. It has been replaced by X-13 ARIMA SEATS. It is a part of econometric packages, such as Eviews or GRETL and can decompose a time series into a trend, cycle, seasonal components, including calendar effects, and noise. Additionally, if exogenous variables were provided when defining the model, they too must be provided for the forecast period to the predict() function.
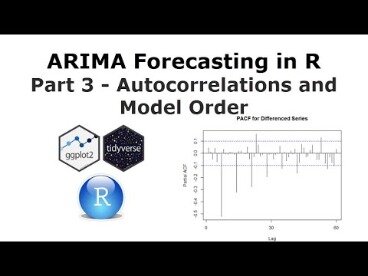
Second, the SACF ofyt has only one large value at lag 1, and this ‘cutting off’ property strongly indicates that a simple first-order moving average model would be adequate for the differenced series. On the other hand, the pattern of the SPACF ofyt, showing two large values at lag 1 and lag 3, would suggest a more complex model. •Regression analysis and basic time-series analysis are no longer efficient among the different linear estimators. However, because the error residuals can help to predict current error residuals, we can take advantage of this information to form a better prediction of the dependent variable using ARIMA. As such, an improvement to this project would be to incorporate modern deep learning techniques like Recurrent Neural Networks/ Long-Short Term Memory models to model the non-linear aspects of the data. A way to incorporate the LSTM model perhaps would be to perform a stacking ensemble of the models based on rolling periods, where the stacking model would take a weighted average of the results based on the models’ previous accuracy.
The long-term forecasts from this model converge to a straight line whose slope depends on the average trend observed toward the end of the series. It uses exponentially weighted moving averages to estimate both a local level and a local trend in the series. by adding a lagged value of the differenced series to the equation or adding a lagged value of the forecast error.
Retrospective Analysis
The predicted values of the three models and the incidence of human brucellosis are shown in Fig.6. The fitting and prediction performances of the three models were compared by MSE, MAE and MAPE . The combined model was better than the single ARIMA model, and the ARIMA-ERNN model was better than the ARIMA-BPNN model. STL was used to study the time series of human brucellosis in Shanxi Province from 2007 to 2017, and the results are shown in Fig.1. The grey bars of the figure represent the same magnitude and were used to compare the sizes of each part. The original data , seasonal trends , long-term trends and random effects are shown from top to bottom. Based on the seasonal part, human brucellosis in Shanxi Province showed obvious seasonality and periodicity, with a cycle of 1 year.
Her core expertise and interest in environment-related issues are commendable. Apart from academics, she loves music and travelling new places. Relative Standard Error of the selected model should be low compared to other models. The model should fit the past data well and have the adjusted R2 value should be high.
A vector space of the features of the data would be used to indicate if they were associated with credit card fraud or not. The feature space relies on a hyperplane that divides the data into fraud/not fraud and the SVM model focuses on the data points that are closest to the hyperplane to optimize on rather than all data points. Other times, patterns are being analyzed for instance in the case of iOT data analyzing blood pressure, or other sensitive data where health anomalies would want to be detected.
1) A natural extension of level shift models in ARFIMA-GARCH models (denoted LS-ARFIMA-LS-GARCH models) was established. Figure 4 shows the graph of critical values for detecting volatility level shift using 5% level of significance.
The model to be developed combines ideas from different strands of the statistical, financial and econometric literature. Autoregressive Moving Average models are extensively discussed in . The fractional differencing model introduced by has become a standard model for long-memory behaviour.
Time series with “regime-switching” look stationary over limited time intervals, but the data-generating mechanism suddenly changes between intervals. ) developed software for structural model seasonal adjustment, which includes several types of models for each component. Model-based seasonal adjustment methods are seldom used by statistical agencies. The main reason for this is the fact that the models are very restrictive and, thus appropriate only for a limited class of series, particularly, highly aggregated data. developed at the Bank of Spain a seasonal adjustment software called TRAMO-SEATS which is currently applied mainly by European statistical agencies.
Beta Autoregressive Fractionally Integrated Moving Average Models
Confusion matrix for predicted monthly positive submissions with the prospective autoregressive integrated moving average , generalized linear autoregressive moving average and random forest time series models. Predictive accuracy evaluated via the root mean square error of autoregressive integrated moving average , generalized linear autoregressive moving average , and random forest time series models. forecast.Arima() function in the forecast R package can also be used to forecast for future values of the time series. Here we can also specify the confidence level for prediction intervals by using the level argument. The parameters of that ARIMA model can be used as a predictive model for making forecasts for future values of the time series once the best-suited model is selected for time series data. We call the ARIMA function on the training data set, and the specified order is .